In 2016 the National Bank of Ukraine (NBU) moved de facto to an inflation targeting regime. One of the required preconditions for successful implementation of an inflation targeting regime is the development of models capable of producing accurate and well-grounded forecasts. In this framework forecasting inflation becomes an essential task.

Regular medium-term macroeconomic forecasts and monetary policy recommendations at the National Bank of Ukraine are mostly based on a Quarterly Projection Model, which is a semi-structural, forward-looking New-Keynesian model of a small open economy. Owing to the fact that the main role of the Quarterly Projection Model is to produce story-telling and to incorporate some expert judgments, the issue of the forecasts’ accuracy may fade into the background. For that reason, it is worth having an additional empirical model producing more accurate forecasts.

A Bayesian Vector Autoregression (BVAR) model for forecasting inflation in Ukraine was developed. The forecasting performance of the model was examined and the accuracy of the forecasts was compared against the forecasts of the Quarterly Projection Model and official NBU forecasts.

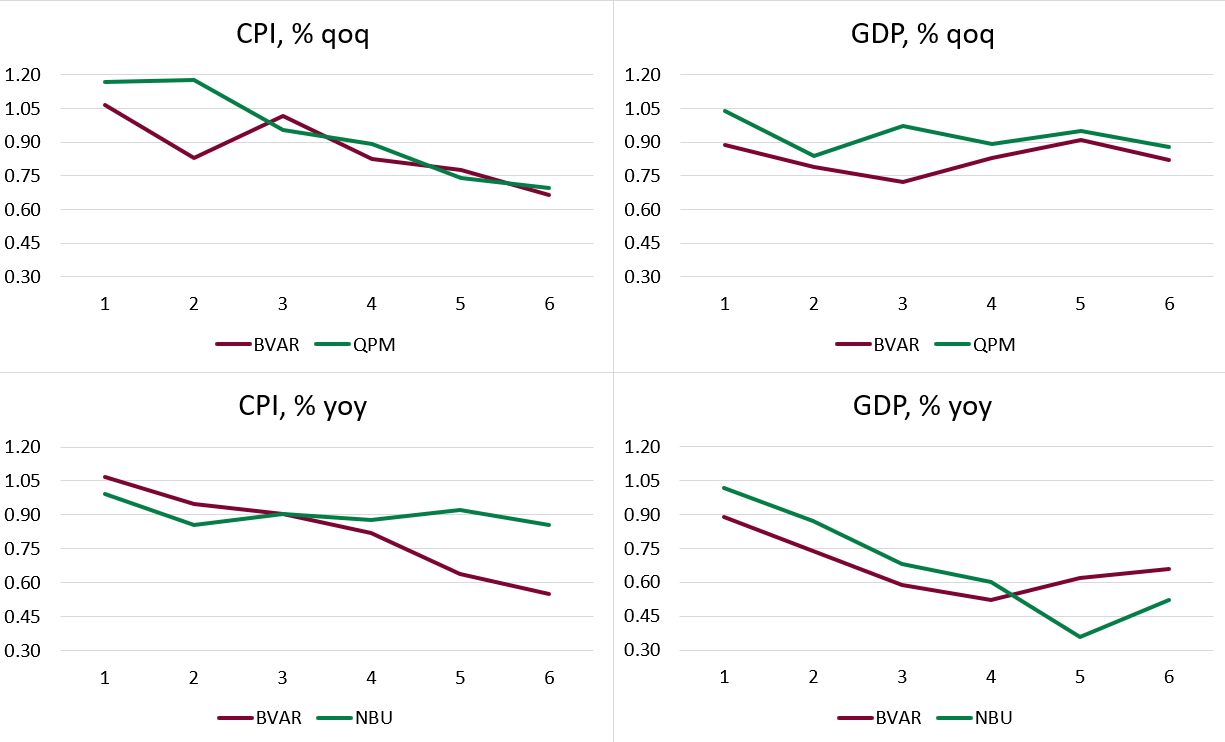
Figure 1. RMSEs relative to the AR1 model.

A Bayesian approach to estimation was chosen given that Ukrainian data is short and dimensionality problems may arise with the large number of parameters present in the model. The imposition of priors not only solves the dimensionality problem but supplements the information contained in the data with the personal judgments contained in the prior. Specifically, a BVAR model with an informative steady- state prior was employed, because this type of priors is widely used for inflation forecasting in countries which adopted an inflation targeting regime, as it explicitly uses information about the inflation target and other equilibrium values. Villani (2009) was the first who imposed prior directly on the steady state of the model. BVAR with steady-state prior was also employed by Iversen et al. (2016), Brázdik and Franta (2017), Beechey and Österholm (2010).

Figure 1 shows the relative RMSEs of the forecasts. The inflation forecasts produced by the BVAR model are more accurate than those of the Quarterly Projection Model two quarters ahead and are competitive for the longer horizon. For GDP growth, the forecasts of the BVAR outperform those of the Quarterly Projection Model for the whole forecast horizon. As NBU forecasts are only available on the year-over-year basis, the forecasts of the BVAR model were transformed from annualized quarter-over-quarter indicators into year-over-year indicators and compared with official NBU forecasts. For inflation the BVAR forecasts outperform the official NBU forecasts over the horizon of three to six quarters ahead. Whereas the opposite is true for the forecasts of the GDP growth over the horizon of five to six quarters ahead.

It should be noted that due to the very short period used for forecasting evaluation exercise, the findings of the research should be treated with caution and might be subject to change as the data accumulates.

To sum up, BVAR models with steady-state prior can be viewed as an effective tool to improve the forecasting accuracy of standard models as they explicitly use information about the inflation target and other equilibrium values.

References

1. Beechey M., Österholm P., (2010). Forecasting inflation in an inflation-targeting regime: A role for informative steady-state priors, International Journal of Forecasting, Elsevier, vol. 26(2), pages 248-264, April.
2. Brazdik F., Franta M., (2017). A BVAR Model for Forecasting of Czech Inflation, Working Papers 2017/7, Czech National Bank.
3. Iversen, J., Laseen, S., Lundvall, H. and Söderström. U. (2016). Real-Time Forecasting for Monetary Policy Analysis: The Case of Sveriges Riksbank. CEPR Discussion Papers 11203, C.E.P.R. Discussion Papers.
4. Villani M., (2009). Steady-state priors for vector autoregressions, Journal of Applied Econometrics, John Wiley & Sons, Ltd., vol. 24(4), pages 630-650.